1. How many different ways are possible to have $k-tuple$ with non-negative integer values such that they sum to a given value $n$?
$\to $To arrive at the solution, one can use the $stars-and-bars$ method. Let’s draw a sequence of n stars. There are $n-1$ spaces between the stars. What we need to do now to create $k$ numbers, is to place $k-1$ bars in those spaces. One such possibility for $n=6$ and $k=3$ is as follows:
\[\star\ | \star\ \star\ \star\ | \star\ \star \quad \quad \to 3-tuple\ (1, 3, 2)\]Thus we need to choose $k-1$ locations out of the $n-1$ spaces available. The number of such combinations possible is thus $\binom{n-1}{k-1}$.
2. What if we allowed for the values to be 0? How many combinations are possible then?
$\to$ In the above case when all is done we placed $n+k-1$ objects(stars + bars). We were restricted by the fact that the values had to be non-negative. So we had to place the bars in the gaps between stars. However, now we do not have any such restriction. We can first choose $k-1$ slots out of $n+k-1$ slots available to place the bars. Once that is done, we just place the $n$ stars in the $n$ slots remaining. One such possibility for $n=6$ and $k=3$ is as follows:
\[\underset{\_}{|}\ \underset{\_}{\star}\ \underset{\_}{\star}\ \underset{\_}{\star}\ \underset{\_}{|}\ \underset{\_}{\star}\ \underset{\_}{\star}\ \underset{\_}{\star} \quad \quad \to 3-tuple\ (0, 3, 3)\]Given this discussion, the number of combinations of $k-tuple$ possible is $\binom{n+k-1}{k-1} = \binom{n+k-1}{n}$. This number is also known as the multiset coefficient.
3. We roll a fair dice $n$ times. What is the probability that all faces have appeared?
Lets $\mathcal{I_i}$ be the number of times a face $i$ has appeared after the dice has been rolled $n$ times. What we need is a $6-tuple\ (\mathcal{I_1}, \mathcal{I_2}, \mathcal{I_3}, \mathcal{I_4}, \mathcal{I_5}, \mathcal{I_6})$ such that the elements sum to $n$, and none of the values $\mathcal{I_i}$ are 0. The probability that all faces have appeared is then the result given in Que. 1 divided by the results given in Que 2.
\begin{align} prob = \binom{n-1}{k-1} / \binom{n+k-1}{k-1} &= \frac{n!\ (n-1)!}{(n-k)!\ (n+k-1)!}\\ &= \frac{n!\ (n-1)!}{(n-6)!\ (n+5)!} \qquad \qquad k = 6 \end{align}
The tail sum for expectation formula for a non-negative integer random number is given as:
\[E[X] = \sum_{x=0}^\infty x\ P(X = x) = \sum_{x=0}^\infty P(X > x)\]Proof: To show this, one can use an interesting identity for any non-negative integer given by:
\[x = \sum_{k=0}^\infty \mathcal{I}(x > k),\]where $\mathcal{I}(condition)$ is an indicator function that evaluates to $1$ if condition is true, else 0. The well known formula for expectation can then becomes:
\[E[X] = \sum_{x=0}^\infty x\ P(X = x) = \sum_{x=0}^\infty \sum_{k=0}^\infty \mathcal{I}(x > k)\ P(X = x).\]Switching the order of summation, we get the required result:
\[E[X] = \sum_{k=0}^\infty \sum_{x=0}^\infty \mathcal{I}(x > k)\ P(X = x) = \sum_{k=0}^\infty P(X > k).\]4. We draw a random number from Uniform distribution $\mathcal{U}[0, 1]$ and keep drawing till the sum of the draws is greater than or equal 1. On average how many samples would we need to draw?
If we independently draw $d$ times from Uniform distribution $\mathcal{U}[0, 1]$, the state-space of all possibilities correspond to the region $S$ in the following diagram (shown for $d=2$ and $d=3$):
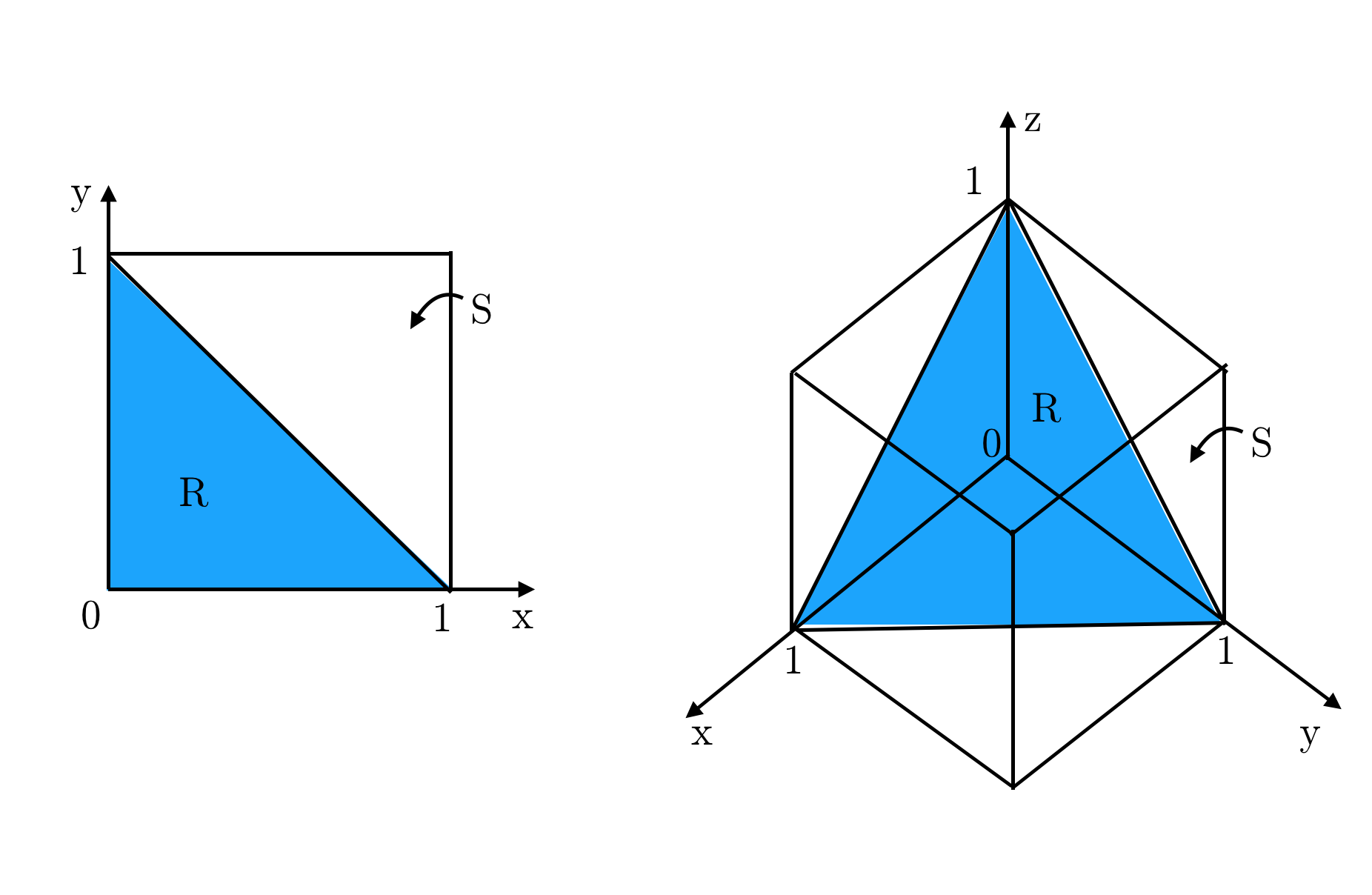
Each point in the region has equal probability. The state-space where the sum of the two draw is less than $1$ is then given by the region $R$. The probability that the sum of the samples drawn is less than $1$ is then the volume of $R$ divided by the volume of $S$.
The region $S$ is nothing but a hypercube in $d$-dimensions where $d$ is the number of draws. For $d=2$, it is a square, for $d=3$ it is a cube and so on. Since each side of this hypercube has length $1$, the volume of $S$ is trivially $1$.
The region $R$ in $d$-dimensions is nothing but a standard $d-simplex$.
The volume of such a simplex can be shown to be $\frac{1}{d!}$.
We can easily verify this for a couple of dimensions.
\begin{align} Vol(2-simplex) &= \int_{x=0}^1 \int_{y=0}^{1-x} dx\ dy = 1/2! \\ Vol(3-simplex) &= \int_{x=0}^1 \int_{y=0}^{1-x} \int_{z=0}^{1-x-y} dx\ dy\ dz = 1/3! \end{align}
Let us now define the random variable whose expectation we require as $X$. In other words, $X=x$ means that we require $x$ draws from the distribution such that the cumulative sum of the draws is greater than or equal to $1$.
\[E[X] = \sum_{x=0}^\infty x\ P(X = x)\]Using the tail sum for expectation, we can write:
\[E[X] = \sum_{x=0}^\infty P(X > x)\]$P(X > x)$ means the probability that one requires more than $x$ draws to reach a sum greater than $1$. This can also be thought as the probability that in $x$ rolls, one obtained a sum less than $1$. Interestingly, this value is nothing but the volume of region $R$. Thus we have
\[E[X] = \sum_{x=0}^\infty P(X > x) = \sum_{x=0}^\infty \frac{1}{x!} = e \quad \quad (surprise!!!)\]Thus, the average number of draws required till the cumulative sum of the draws is greater than or equal to $1$ is $e$.