One of the most basic things that one can do with an array is to have a pointer or a set of pointers that traverse the array in some fashion. The number of pointers to book-keep depends on the question at hand. Let’s look at few sample problems to understand this concept:
- Given an array nums compute the largest element.
To find the largest element, we have to at-least visit each element in the array. Thus we need a single pointer to traverse the array. We will reserve a constant memory space that holds the value of the largest element or at least the index of the position that holds the largest element.
def get_largest(nums: List[int]) -> int:
largest_num = float('-inf')
for num in nums:
largest_num = max(largest_num, num)
return -1 if largest_num == float('-inf') else largest_num
- Given an array nums and a target check if target exists in the array.
Since we are not given any extra information as to the structure of the array, e.g. sorted or not, we should write a solution for the generic case. Similar to the previous case, we need a pointer that scans through the array and at each step check for equality of the element with the target. This gives us $O(n)$ time complexity and $O(1)$ space complexity algorithm as follows:
def find_target(nums: List[int], target: int) -> bool:
for num in nums:
if num == target:
return True
return False
Here is a slightly complicated problem, where we have a single traversal pointer: given a linked list, reverse it.
def rev_linked_list(head):
new_head = None
while head is not None:
next_in_line = head.next
head.next, new_head = new_head, head
head = next_in_line
return new_head
- Given a sorted array nums and a target check if there exists $(i, j)$ such that $nums[i] + nums[j] = target$ and $i \ne j$.
Since we need to find two elements from the array that sum to the target, we should probably use two pointers. But the questions is where should they be placed initially. Ideally we would like to, on each iteration, update one or both the pointers and the updates should be such that we march towards the breaking or end-of-iteration criteria. In this case, we should place one pointer at the beginning and the other at the end. We will call them left and right respectively. If the sum of the elements at these positions is greater than the target, then the only way to bring down the sum is to decrease the right pointer. Conversly, if the sum is smaller than the target, the only way to increase the sum is to update the left pointer. Note that the we can make the above two statements only in this specific case of sorted array. If they sum to the target, we have found the pair and simply exit the iteration.
def two_sum_sorted(nums: List[int], target: int) -> bool:
left, right = 0, len(nums) - 1
while left < right:
curr_sum = nums[left] + nums[right]
if curr_sum == target:
return True
elif curr_sum > target:
right -= 1
else:
left += 1
return False
- You are given an integer array nums of length n; such that each element represent a height of a column placed at that index, with the base resting on the $x-axis$. Find two lines that together with the x-axis form a container, such that the container contains the most water and return the maximum amount of water a container can store.
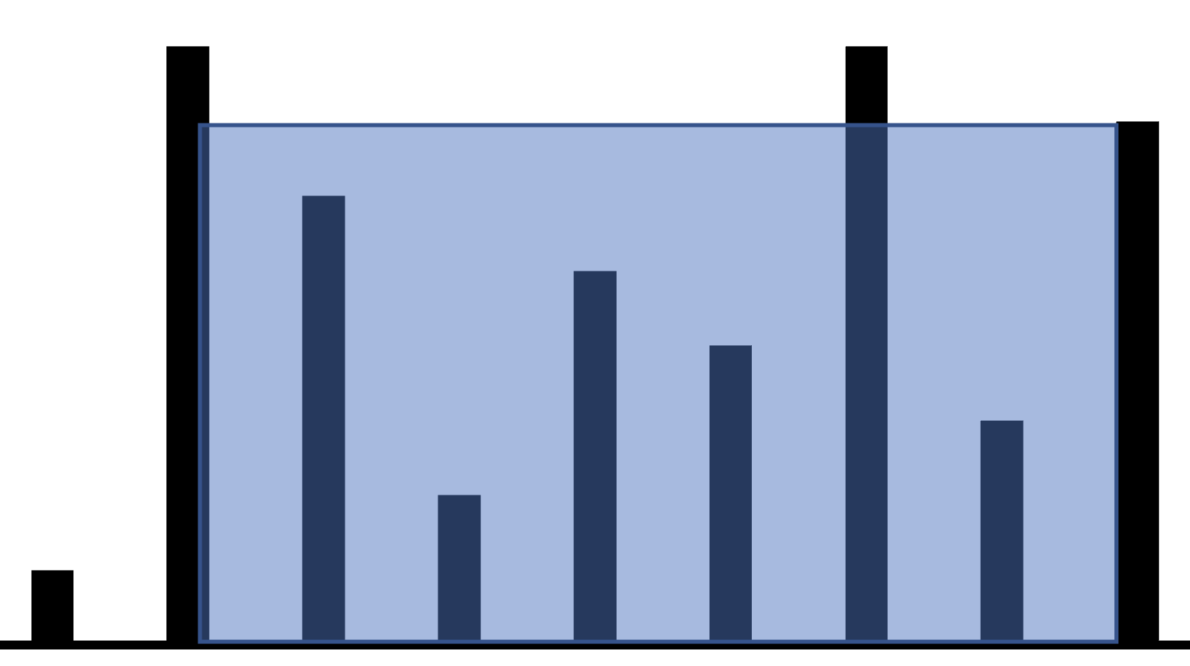
Since we need to create a container, we need two columns and hence two pointers, the left and the right column of the container places at indices $i$ and $j$, such that $i < j$. Now the question is what should be the initial placement of these pointers.
We actually only have 2 sensible choices:
- One after other $i=0, j=1$
- Opposite ends $i=0, j=len(nums) - 1$.
At any given configuration $(i, j)$, the volume of the water contained is: $V = width \times height = (j - i) * min(nums[i], nums[j])$.
If we place the pointers at opposite ends, then in every iteration we will either increment $i$ or decrement $j$, i.e. the width will always decrease. Hence the only hope of finding the container with more water is to increase the height. Since the height of the water volume is controlled by the smaller of the two columns, the pointer of the column which is smallest should be updated.
If instead we had chosen the one-after-other configuration, then in each iteration, the width will either decrease or increase and we won’t be able to make a decision as to which pointer to update as we did above.
def most_water_container(heights: List[int]) -> int:
max_water_content = float('-inf')
left, right = 0, len(heights) - 1
while left < right:
# Water content = width * (bar with the lower height of the two)
water_content = (right - left) * min(heights[left], heights[right])
max_water_content = max(max_water_content, water_content)
# Which pointer to update? We will be making the width smaller with
# the next pointer update, so the only hope for increasing the water content
# is to increse the minimum height. Hence we should update the pointer
# of the bar with the lower height of the two.
if heights[left] < heights[right]:
left += 1
else:
right -= 1
return max_water_content
Kadane’s Algorithm
Let’s say we are given an array of integers; the goal is to find a subarray with the maximum sum.
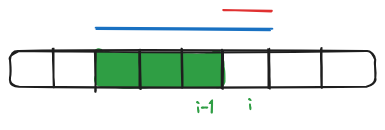
To do this we find the subarray that starts at any given index, but ends on the index being considered; and we do this for every index. Let’s say that we have a such a subarray that ends on index $i-1$; shown in green. Now what would be the max subarray that ends on index $i$. Well we have two options: either we extend the previous subarray (blue) or we go solo i.e. start anew (red). Once we have the max subarrays ending at each index, the result will be the one that has the maximum value.
def max_sum_subarray(nums):
curr_sum, max_sum = nums[0], nums[0]
for i in range(1, len(nums)):
curr_sum = max(curr_sum + nums[i], nums[i])
max_sum = max(max_sum, curr_sum)
return max_sum
The above algorithm will give the max subarray sum. However, if we also wanted the subarray [left index, right index] that had that sum, we have to modify the algorithm a little bit.
Basically we keep track of the ending index of the max subarray. Then we traverse the array in the backward direction starting at the ending index,
until we find the element that started the subarray.
def max_sum_subarray(nums):
ending_idx = 0
curr_sum, max_sum = nums[0], nums[0]
for i in range(1, len(nums)):
curr_sum = max(curr_sum + nums[i], nums[i])
if curr_sum > max_sum:
ending_idx = i
max_sum = curr_sum
# traverse back to find the start index
last_sum, start_idx = max_sum, ending_idx
while last_sum != nums[start_idx]:
last_sum -= nums[start_idx]
start_idx -= 1
return start_idx, ending_idx, max_sum