To uniformly sample points over a volume one needs to consider the infinitesimal volume element corresponding to that specific geometry in a given coordinate system.
For example, let’s consider uniformly sampling points over a linear geometry between a and b. The infinitesimal volume (in this case line) element is simply given by
$dV = dx$. In this case, one can trivially get the corresponding points using: $pt = \mathcal{U}[0, 1] * (b - a) + a$.
import numpy as np
pts = np.random.rand(100) * 3 + 2 # 100 pts between 2 and 5
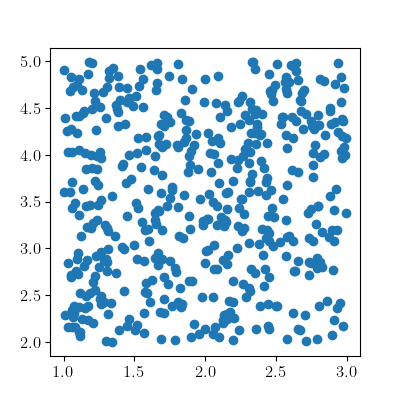
What if we have to sample uniformly over a square in the range $x \in [1, 3)$ and $y \in [2, 5)$. The infinitesimal volume (in this case area) element in cartesian coordinate system is given by $dV = dx\ dy$. Since it can be written as a product of infinitesimal line elements for each dimension, one can randomly sample points independently across each dimension.
pts_x = np.random.rand(1000) * 2 + 1
pts_y = np.random.rand(1000) * 3 + 2
Now let’s say we have to sample points uniformly within a circular region of radius $r_{max}$. If working in cartesian coordinate system, one can first sample point uniformly in the 2D square as above with the extents $[-r_{max}, r_{max}]$ and then only keep the point if it lies within the circular region i.e. $x^2 + y^2 \le r_{max}^2$. This will give the correct result; however, its a little wasteful in the sense that on average we would have to sample $n_{pts} \left[ 1 + \frac{\pi}{4}\right]$ points before we reach the required number of points.
A better and more efficient approach would to be work in the circular coordinate system $(r, \theta)$. Naively one might think to uniformly sample points with $r \in [0, r_{max}]$ and $\theta \in [0, 2 \pi]$; and them transforming them to $x$ and $y$ using:
\[x = r \cos \theta \qquad y = r \sin \theta\]Here is the result with $r_{max} = 4$
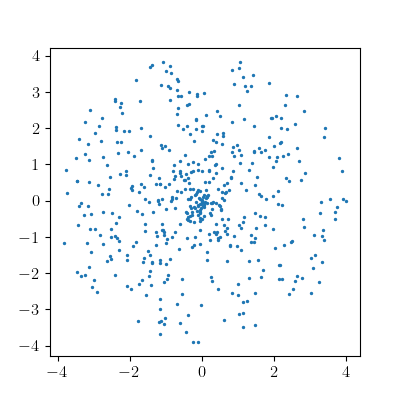
However, using this strategy we don’t get uniform distribution. Points are over-sampled as one goes radially inwards. A correct approach is to look at the infinitesimal volume element in spherical coordinate system, which is
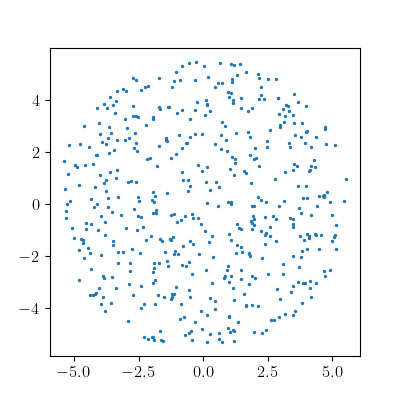
\[dV = r\ dr \ d\theta = d \left(\frac{r^2}{2} \right)\ d\theta = dr'\ d\theta\]One can then uniformly sample in $r’$ where $r’ = r^2 / 2$ and in $\theta$. In the case of $r_{max} = 4$, this implies sampling $r’$ uniformly over the range $r’ \in [0, 16)$.
pts_r_prime = np.random.random(500) * 16
pts_theta = np.random.random(500) * 2 * np.pi
pts_r = np.sqrt(2 * pts_r_prime)
pts_x = pts_r * np.sin(pts_theta)
pts_y = pts_r * np.cos(pts_theta)
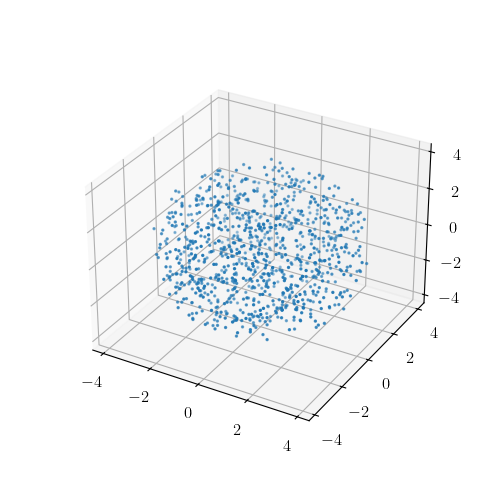
What if we go up a dimension and have to sample points uniformly within a spherical volume till $r = r_{max}$. In spherical coordinate system, the infinitesimal volume element is given by:
\[dV = r^2 \sin \theta\ dr\ d\theta\ d\phi = [ d(r^3/3)]\ [d\cos \theta]\ [d\phi]\]Thus we have to:
- Uniformly sample in $\phi \in [0, 2 \pi]$
- Uniformly sample in $\cos \theta$. Since $\theta$ goes from 0 to $\pi$, we have to sample $\cos \theta \in [1, -1]$.
- Uniformly sample in $r’ \in [0, r_{max}^3 / 3]$, where $r’ = r^3 / 3$
$\rightarrow$ If we have a coordinate system $(u_1, u_2, u_3)$ that is related to the cartesian coordinate system via some transforms $x = f(u_1, u_2, u_3), y = g(u_1, u_2, u_3), z=h(u_1, u_2, u_3)$; then the infinitesimal volume element in the new coordinate system is given by:
\[dV = \left| \frac{\partial(x, y, z)}{\partial(u_1, u_2, u_3)}\right| du_1\ du_2\ du_3\]