A binary tree is a tree data structure where every node has at most two children.
Each node can be of three categories - the root which has no parent, the leaf which have no children,
and the inner nodes, which have at least one child. A node can be defined as follows:
class TreeNode:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
Here is an example binary tree: 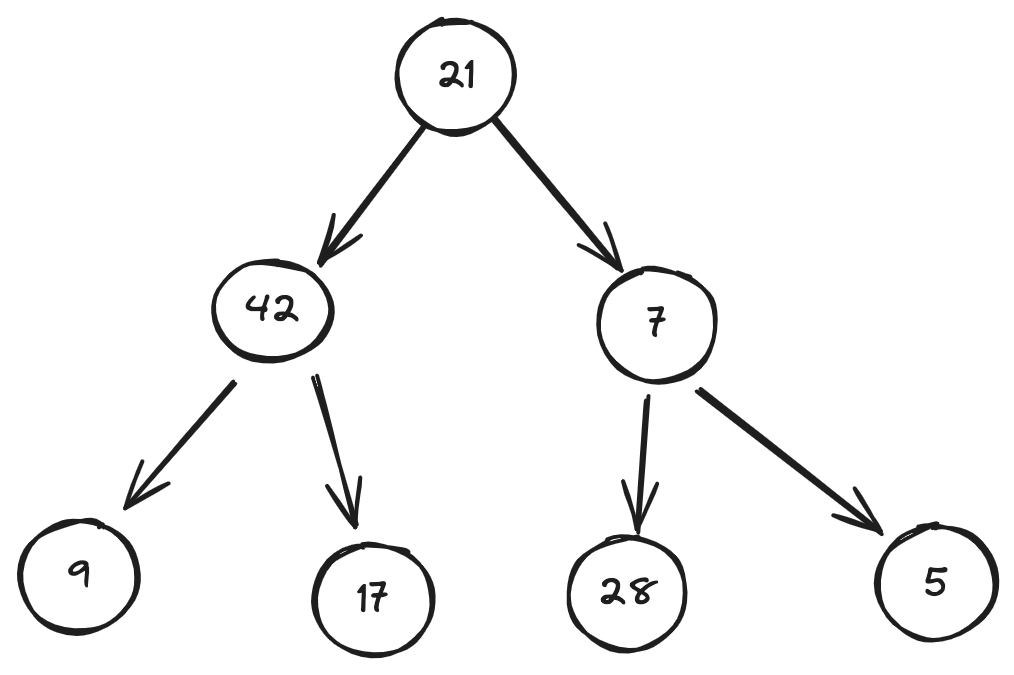
A traversal can be defined as a strategy in which to visit every node of the tree. We can either go wide or go deep.
$\rightarrow$ For the case where we want to go deep first (depth-first traversal), we can define the following three recursive ways depending on when the current node is marked as visited.
- Pre-order traversal
def pre_order_traversal(node) -> None: if node is not None: print(node.val) pre_order_traversal(node.left) pre_order_traversal(node.right) - In-order traversal
def in_order_traversal(node) -> None: if node is not None: in_order_traversal(node.left) print(node.val) in_order_traversal(node.right) - Post-order traversal
def post_order_traversal(node) -> None: if node is not None: post_order_traversal(node.left) post_order_traversal(node.right) print(node.val)
$\rightarrow$ For the case where we want to go wide first (breadth-first search), we can use a queue for the traversal. For more details on queue, refer to this page. Note that this traversal basically prints the values on a per-level basis, hence it is also called as Level-order traversal.
from collections import deque
def bfs(root) -> None:
queue = deque([root])
while queue:
node = queue.popleft()
print(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
Binary Search tree
A binary search tree (BST) is a binary tree where for every node, the value of the left child is less than or equal to the current node value, and the value of the right child is greater than the current node value. Here is one example: 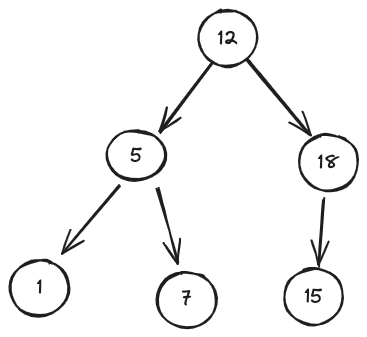
Note: An in-order traversal of a BST will lead to values in sorted order.
Shortest paths
A BFS is very useful when computing shortest paths. Let us consider a binary matrix where the goal is to start at the top-leftmost position and reach the bottom-rightmost position in the shortest amount of steps. A cell can be visited only if the matrix value at that location is 0 and all the adjacent cells of the path are 8-directionally connected (share an edge or a corner)
from collections import deque
def shortest_path_binary(grid):
n, m = len(grid), len(grid[0])
# trivial case: if the starting location itself is invalid
if grid[0][0] == 1:
return -1
queue = deque()
queue.append((0, 0))
len_queue = deque([1])
seen = set((0, 0))
while queue:
node = queue.popleft()
prev_length = len_queue.popleft()
# logic for reaching the destination
if node == (n-1, m-1):
return prev_length
for x, y in [[0, 1], [0, -1], [1, 0], [-1, 0],
[-1, -1], [-1, 1], [1, -1], [1, 1]]:
neighbor = (node[0] + x, node[1] + y)
if (
(neighbor[0] >= 0) and # boundry condition
(neighbor[0] < n) and
(neighbor[1] >= 0) and
(neighbor[1] < m) and
(grid[neighbor[0]][neighbor[1]] == 1) and # visit condition
(neighbor not in seen) # avoid looping back
):
seen.add(neighbor)
queue.append(neighbor)
len_queue.append(prev_length + 1)
# if we reach here, we haven't found any path
return -1
from collections import deque
def shortest_path(start):
""" Shortest path from start to every other vertex.
"""
shortest_path_map = {start: 0}
queue = deque([start])
while queue:
curr_node = node.popleft()
for child, weight in zip(curr_node.children, curr_node.weights):
connceted_path_length = weight + shortest_path_map[curr_node]
if child not in shortest_path_map:
shortest_path_map[child] = connected_path_length
queue.append(child)
else:
if shortest_path_map[child] > connected_path_length:
shortest_path_map[chid] = connected_path_length
queue.append(child)
return shortest_path_map